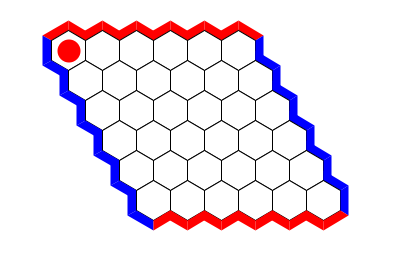
A1 opening

The title given to this article is incorrect due to technical limitations. The correct title is a1 opening.

The a1 opening (in the acute corner) is one of only two openings known to be defeatable. The other is b1.

(This does not mean that these are the worst possible opening moves. Compare with the diagrams on the openings page at the queenbee site)

Like the proof that Hex is a win for the first player, the proof that A1 loses is non-constructive: Although we know that it exists, the winning strategy has not been found for regular sized Hex boards.

Due to the symmetry of the Hex board, the same is true of the opposite hexes, but they are not usually referred to explicitly because their designation depends on the size of the board.

Sketch for proof

Let's suppose a1 is a winning first move for Red. There exists a winning strategy for Red beginning with 1.a1.

Blue answers a2, this move makes Red's move useless as b1 does not need a1 to connect to top edge. Blue can now pretend to be the first player.

Every winning connection that would have used the hexe a1 is a winning connection here too thanks to a2. Hence Blue can use Red's winning strategy and win too.

This is absurd and so there is no winning strategy beginning by a1. Therefor 1.a1 is a losing move (because there is no draw possible).

a2 has been proved a losing answer

A sketch of the proof on kosmanor page

References

References for proofs can be found on the Hex Theory page.